Tempo de leitura: 5 minutos
Se você está começando a programar, já programa ou se é um programador da
época do MS DOS, você com certeza já ouviu falar do Insertion Sort. Um dos
métodos mais amados da comunidade, mas com uma eficiência que não enche
os olhos ( O(n^2)). Vamos ver como ele funciona?
O Que é o Insertion Sort?
Todo o conceito do Insertion Sort é, como o próprio nome nos diz, inserir elementos de forma ordenada. Assim, cada elemento do array deve ser adicionado na posição correta. Ainda confuso? Calma, vamos entender melhor.
Imagine que você está jogando um jogo de cartas e que você deseja sempre manter as cartas organizadas na sua mão. Isso é perfeito para que você jogue bem durante a partida. Preparado? Vamos lá.
Você acaba de receber 4 cartas, que aqui serão as cartas de valores 2, 4, 6 e 10. Logo que as recebe, elas estão embaralhadas e você decide ordená-las por ordem crescente. Feito? Então vamos em frente.
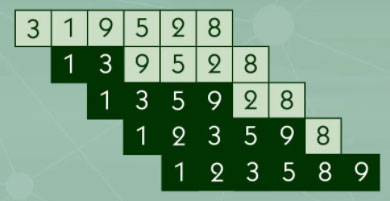
Infelizmente, em uma rodada hipotética, você terá que receber uma carta a mais. Você não sabe, obviamente, o valor da carta que virá. O que fazer para inserir a carta de forma ordenada? Insertion Sort tem a solução.
Que tal você analisar o valor desta carta e comparar com cada uma das que estão na sua mão? Boa ideia não é?! Perfeito, então imaginemos que a sua carta recebida foi a de valor 3. Ela será a sua referência agora e é a partir dela que realizaremos as comparações. Você analisa e percebe que ela deve estar na posição entre o 2 e o 4.
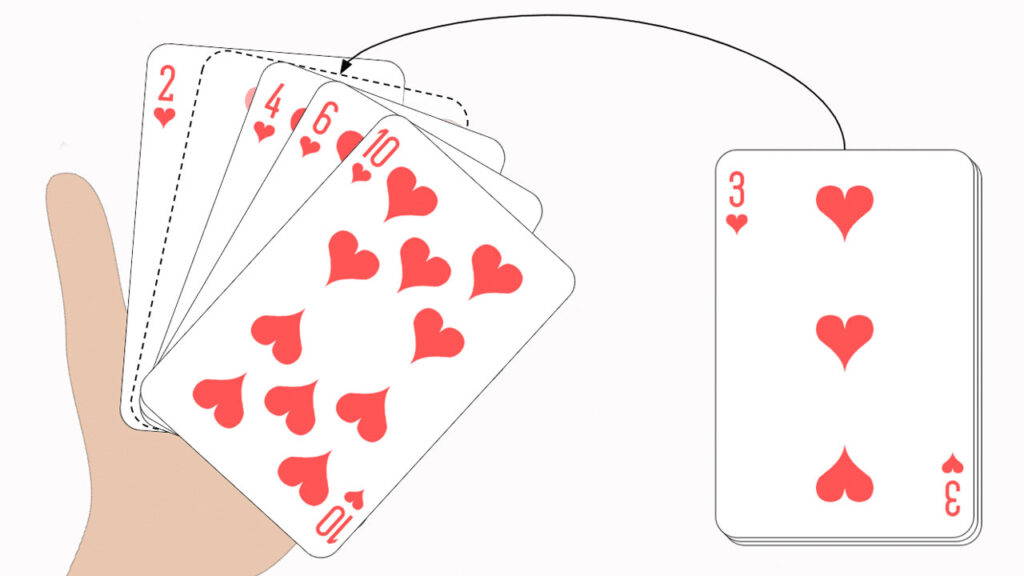
Agora que você já sabe onde a carta deve se encaixar, o que você faz? Bom, basta afastarmos as cartas que temos na mão para os lados e adicionarmos a nossa nova carta. Você acabou de usar o algoritmo de Insertion Sort. Parabéns!
Brincadeiras à parte, vamos ao código, afinal, um programa não se constrói com cartas.
Mão no Código
Agora que você já entendeu como funciona o Insertion Sort, usaremos a linguagem Javascript para apresentar o código inicial desse método de ordenação. Primeiro deixarei o código completo e depois analisaremos parte a parte.
function insertionSort(array) {
let n = array.length;
for (let i = 1; i < n; i++) {
let atual = array[i];
let j = i - 1;
while (j > -1 && atual < array[j]) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = atual;
}
return array;
}Passo a Passo
Linhas 1-2
function insertionSort(array) {
let n = array.length;Aqui iniciamos a nossa função com nome insertionSort, que receberá um elemento que chamaremos de array. É este array que iremos ordenar e ao fim devolver ordenado.
Na linha seguinte, declaramos como n o tamanho do nosso array. Isto será importante para a nossa condição de parada do loop.
Linha 3
for (let i = 1; i < n; i++) {Nesta linha iniciamos a iteração por todo o array. Começamos definindo a nossa variável i=1, com paragem quando for igual ao tamanho do array e incremento de 1 valor.
A primeira pergunta ao analisar este loop é: por que começar pelo 1? Ora pequeno gafanhoto, por definição o insertion sort começa pelo segundo elemento. Somente assim podemos comparar um valor com o seu anterior, afinal array[0] nunca poderia ser comparado com array[-1]. Lembre-se que todo array começa na posição 0, ao menos na grande maioria das linguagens, logo a posição array[-1] não existe!
Linhas 4-5
let atual = array[i];
let j = i-1; Agora vamos declarar estas que serão as variáveis fundamentais do Insertion Sort. Chamaremos de atual o valor que estamos do array e de j o valor de índice anterior ao que estamos.
Vamos ao exemplo: No array [1, 8, 4, 6] a nossa variável atual será inicialmente array[1], ou seja, 8. O nosso j será 1-1, ou seja, j=0 e array[j] =1;
Linha 6
while ((j > -1) && (atual < array[j])) {Já temos o valor de j e da variável atual, agora vamos para mais uma iteração. Finalmente, realizaremos as trocas para a ordenação do array.
Iniciamos o loop while garantindo que o nosso j não pode ser igual a -1, afinal, arrays, em javascript, tem como início o índice zero. Tendo isto em conta, continuemos.
Como estamos ordenando em ordem crescente, queremos que: se o meu valor atual for menor do que o número anterior a ele, entramos no loop while e trocamos os dois de posições. A condição atual<array[ j ] garante exatamente isso.
Linhas 7-8
array[j+1] = array[j];
j--;Vamos agora supor que você tem valor atual=8 e array[ j ]=1, sendo assim entramos no loop e observamos a troca.
O array de index j+1, receberá o meu array[ j ] e o meu j diminuirá 1 valor de tamanho (j–), assim posso continuar a comparação para os elementos antecessores ao j inicial, que era de i-1.
Perceba que, assim que este loop parar, eu consigo encontrar a posição ideal para a minha variável atual e é exatamente o que faremos.
Linhas 10-12
array[j+1] = atual;
}
return array;Ao sair do loop, declaramos array[ j+1] = atual e iteramos novamente o valor de i, agora incrementado. Ao final do loop for, devolvemos o array completamente ordenado.
Conclusão
Como vimos, o Insertion Sort é um algoritmo de fácil implementação, simples entendimento e, como já havia dito, de eficiência baixa. Mas o que quer dizer eficiência baixa?
Em resumo, a eficiência do Insertion Sort é fraca pois ele utiliza 2 loops, o que não é bom para arrays muito grandes, com um length de 100000, por exemplo.
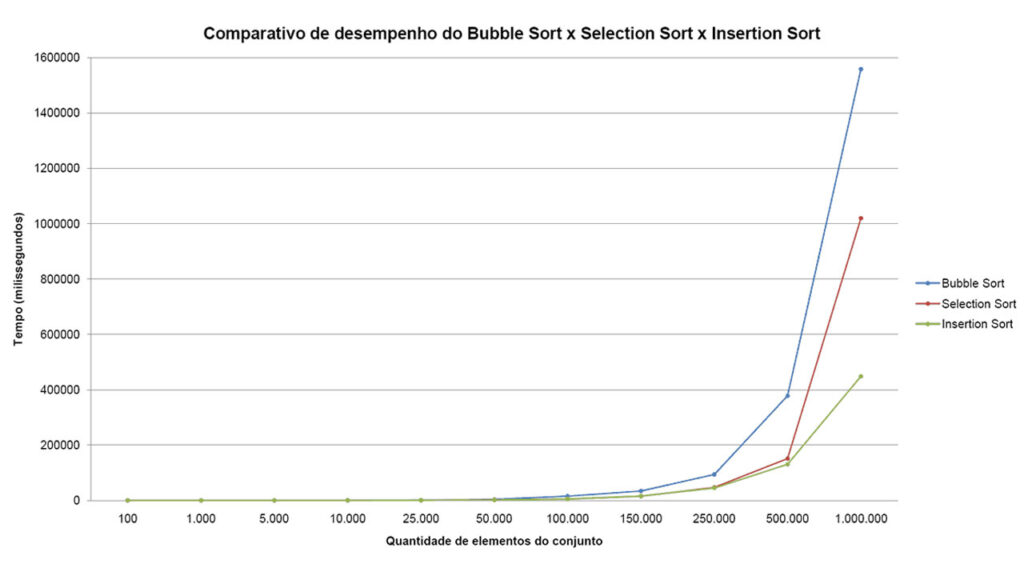
Este método de ordenação, no entanto, é muito utilizado para arrays de tamanho pequeno, já que, nestas condições, performa melhor do que a maioria dos outros métodos. O próprio Chrome e o Mozilla se utilizam de métodos mais complexos de ordenação para arrays grandes e Insertion Sort para organização de arrays pequenos.
Dada a sua importância, o Insertion Sort é uma das mais simples e importantes formas de ordenação de arrays. É utilizado por diversos projetos e ensinado em qualquer curso de desenvolvimento de software. Você com certeza vai usá-lo, mas não abuse. Utilize para aquilo que ele foi criado: arrays pequenos.
